시뮬레이션 학습로그

시뮬레이션이란 무엇일까?

목차

1. 배경
2. 공유지의 비극 (Tragedy of the commons)
   • 모델링
3. 인과 루프 다이어그램 (Causal Loop Diagram)
   • 구성 요소
   • 루프의 종류
   • Delays
4. 시스템 원형 (System archetype)
   • 에스컬레이션 (Escalation)
   • 성공은 성공을 낳는다 (Success to Successful)
5. 인과 루프 다이어그램에서 동적 시스템 모델로 Causal loop diagram to system dynamics model
   • 주요 단계
   • 예시: 인구 성장 모델
6. Simulation time flow and finite state machine
   • 시뮬레이션 시간 흐름 (Simulation time flow)
   • 유한 상태 기계 (Finite state machine)
     • 주요 구성 요소
     • 특징
     • 예시: 자동 판매기
   • 시뮬레이션에서의 활용

배경

이 글에서는 시뮬레이션 및 모델링의 기초를 살펴볼 예정입니다. 시뮬레이션이란 무엇일까요? 제가 애용하는 Claude에게 물어본 결과 시뮬레이션은 실제 세계의 시스템, 상태 또는 프로세스를 컴퓨터나 물리적 모델을 통해 모방하는 것 이라고 합니다. 시뮬레이션을 통해 실제 세상을 예측할 수 있다면 정말 유용하지 않을까요?

해당 글은 KAIST의 온라인 공개강좌인 모델링 및 시뮬레이션 개론을 주로 수강하며 작성한 글입니다.

공유지의 비극 (Tragedy of the commons)

세상에는 여러 공공자원이 있습니다. 대표적으로는 물, 땅, 석유 등이 있는데요, 이러한 공유자원들이 따로 관리되지 않고, 개인이 이익에 따라 소비한다면 해당 자원은 고갈되어버린다는 경제 과학적 상황을 공유지의 비극이라고 표현합니다. 이 예시는 시뮬레이션과 모델링을 설명할 때 많이 사용하는 예시입니다.

상황을 가정해봅시다. 목자가 두 명이 있고, 각각 자신의 양떼를 가지고 있습니다. 둘은 일종의 경쟁관계입니다. 양들이 풀을 먹을 수 있는 목초지는 제한되어있다고 할 때, 목자들은 어떤 선택을 해야 자신의 이익을 극대화 할 수 있을까요?

1. 양떼에게 하루종일 풀을 먹인다.
2. 양떼를 늘린다.

등등 여러가지 선택을 할 수 있겠지만, 결과적으로는 공유자원인 목초지를 경쟁자보다 더 빨리, 많이 소비 할 수록 이익이 극대화됩니다. 이러한 선택지를 통해 제한된 공공재를 소비한다면, 결과는 고갈이 될 수밖에 없을 것입니다.

모델링

해당 예시에 대한 모델링을 진행한다면 어떤 방법이 있을까요? 먼저 중요한 오브젝트 객체를 정의 해 봅시다.

1. 목초지
2. 양떼
3. 목자
4. 황폐지

등으로 정의를 할 수 있겠습니다. 하지만 아쉽게도 여기서 끝이 아닙니다. 각 오브젝트의 속성과 관계도 정의해야 합니다.

1. 양떼 크기에 따른 목초지에서 황폐지로의 변화율
2. 시간에 따른 황폐지에서 목초지로의 변화율
3. 양떼의 번식율
4. 전체 목초지의 크기

여기서 정의된 속성/관계는 일부에 불과합니다. 이외에도 고려해야 할 것들이 많습니다.

인과 루프 다이어그램 (Causal Loop Diagram)

Causal loop diagram은 시스템 내의 변수들의 인과 관계를 시각적으로 표현하는 도구입니다. 화살표로 변수 간 관계를 나타내며, 양의 관계(+)와 음의 관계(-)를 구분합니다. 시뮬레이션을 위해 모델링할 때 Causal Loop Diagram을 이용하면 모델의 대략적인 모양(abstracted view)을 관찰할 수 있습니다.

Causal Loop Diagram에는 세 가지 주요 구성 요소가 있습니다:

1. Factors
   • Factors은 수치 변수로, 양이나 강도를 나타냅니다.
2. Relationships between the factors
   • Relationships는 Feedback, Positive/Negative 링크가 있습니다.
3. Delays
   • 지연에 대해서는 나중에 자세히 설명하겠습니다.

긍정적/부정적 링크는 루프를 생성할 수 있으며, 두 가지 종류의 루프가 있습니다:

• 강화 루프(Reinforcing loop) 및
  • 강화 루프는 사이클 내 Negative 링크의 개수가 짝수일 때 나타납니다.

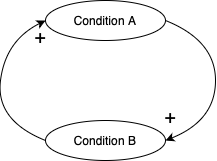
• 균형 루프(Balancing loop)
  • 균형 루프는 Negative 링크의 개수가 홀수일 때 나타납니다.

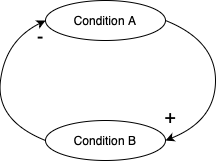
Delays

지연이 없다면 모델링을 간단하게 표현하고 이상적으로 작동하도록 만들 수 있습니다. 하지만 현실세계의 대부분의 문제에는 지연이 포함됩니다.

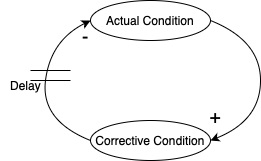
예를 들어, 발주를 넣었는데 상품이 도착하지 않아 계속 발주를 넣는 경우 기대치보다 더 많은 상품이 도착할 수 있습니다. 이 때 이것을 해결하기 위해 반납을 할 수 있는데요, 반납 또한 지연되는 시간이 있기 때문에 발주때와 비슷한 문제가 발생할 수 있습니다. 이것을 진동(oscillations) 이라고 표현합니다.
진동이 목표치에 Converge한다면 목표값에 도달할 수 있지만, 오차가 계속 커지는 상황이 발생한다면 이를 채찍 효과(bullwhip effect)라고 합니다. 이는 주로 공급망 관리(SCM)에서 발생할 수 있는 일반적인 문제입니다.

시스템 원형 (System archetype)

System archetype은 조직이나 시스템에서 반복적으로 나타나는 행동 패턴을 설명하는 개념적 모델입니다. archetype을 이해하면 복잡한 시스템의 문제를 더 쉽게 파악하고 해결할 수 있습니다.

아래의 예시들은 System Archetype에서 이미지와 더 자세한 설명을 확인할 수 있습니다.

Archetype: 에스컬레이션 (Escalation)

이 타입에는 치킨 게임, 군사력 경쟁 등이 포함됩니다. 두 개의 루프 사이에 공통 Factor가 있고, 이 요인이 두 루프를 모두 제어합니다. 예를 들어, A 국가에서 군사력을 증강하면 B 국가도 군사력을 증강해야 하고, 이로 인해 양측에서 지속적인 상승 효과가 발생하게 됩니다.

Archetype: 성공은 성공을 낳는다 (Success to Successful)

이 타입은 한정된 자원 상황에서 A와 B가 있을 때, A에 자원이 투자될수록 B의 힘이 약해지는 현상을 설명합니다. 두 루프 모두 강화 루프이지만, 방향이 다릅니다.

인과 루프 다이어그램에서 동적 시스템 모델로 Causal loop diagram to system dynamics model

Causal Diagram에서는 시나리오를 Conceptual하게 모델링하기에는 좋았지만, 실제 복잡한 문제에서 해당 방식으로 모델링하기에는 복잡도나, 가시성의 문제가 발생합니다. 즉, 정성적 모델에서 정량적 모델로 발전시키기 위해서는 System Dynamics Model로 발전해야합니다. 이 과정에는 변수의 수학적 정의, 초기값 설정, 방정식 구성 등이 포함됩니다.

주요 단계:

1. 변수 식별 및 정의:
   • Causal loop diagram의 각 요소를 명확한 변수로 정의합니다.
   • 각 변수의 유형(stock, flow, auxiliary)을 결정합니다.
2. 수학적 관계 설정:
   • 변수 간의 관계를 수학적 방정식으로 표현합니다.
   • 예: 인구 증가율 = 출생률 - 사망률
3. 초기값 설정:
   • 각 stock 변수의 초기값을 정의합니다.
   • 시뮬레이션 시작 시점의 시스템 상태를 나타냅니다.
4. 시간 단위 및 시뮬레이션 기간 설정:
   • 모델의 시간 단위(예: 일, 월, 년)를 결정합니다.
   • 전체 시뮬레이션 기간을 설정합니다.
5. 함수 및 테이블 정의:
   • 비선형 관계를 표현하기 위한 그래프 함수나 룩업 테이블을 생성합니다.
6. 피드백 루프 구현:
   • Causal loop diagram의 피드백 구조를 수학적 관계로 변환합니다.
7. 지연 효과 모델링:
   • 시스템의 지연 효과를 표현하기 위해 적절한 지연 함수를 사용합니다.

예시: 인구 성장 모델

추가적인 이미지와 예시들은 System Dynamics에서 확인할 수 있습니다.

Causal loop diagram:

출생률 (+) --> 인구 --> (+) 출생률
인구 --> (+) 사망률 --> (-) 인구

System dynamics model:

인구(t) = 인구(t-dt) + (출생률 - 사망률) * dt
초기 인구 = 1000
출생률 = 인구 * 출생률_계수
사망률 = 인구 * 사망률_계수
출생률_계수 = 0.03
사망률_계수 = 0.02

Simulation time flow and finite state machine

시뮬레이션에서 시간은 연속적 또는 이산적으로 모델링될 수 있습니다. 유한 상태 기계는 시스템이 가질 수 있는 상태의 수가 유한하며, 특정 조건에 따라 상태 간 전이가 일어나는 모델입니다.

이 두 개념은 다양한 시스템의 동적 행동을 모델링하는 데 중요한 역할을 합니다.

시뮬레이션 시간 흐름 (Simulation time flow)

시뮬레이션에서 시간의 흐름을 모델링하는 방식은 크게 두 가지로 나눌 수 있습니다:

1. 연속적 시간 흐름 (Continuous time flow):
   • 시간이 끊임없이 연속적으로 흐르는 것으로 모델링합니다.
   • 미분 방정식을 사용하여 시스템의 변화를 표현합니다.
   • 예: 물리 시스템, 화학 반응, 인구 동태 등
2. 이산적 시간 흐름 (Discrete time flow):
   • 시간을 일정한 간격으로 나누어 모델링합니다.
   • 차분 방정식이나 이산 사건을 사용하여 시스템의 변화를 표현합니다.
   • 예: 디지털 시스템, 생산 라인, 컴퓨터 네트워크 등

시간 흐름의 선택은 모델링하려는 시스템의 특성과 시뮬레이션의 목적에 따라 결정됩니다.

유한 상태 기계 (Finite state machine)

유한 상태 기계는 시스템의 동작을 유한한 수의 상태와 그 사이의 전이로 표현하는 수학적 모델입니다.

주요 구성 요소

1. 상태 (States): 시스템이 가질 수 있는 모든 가능한 조건이나 상황
2. 전이 (Transitions): 한 상태에서 다른 상태로의 변화
3. 이벤트 (Events): 전이를 트리거하는 조건이나 입력
4. 액션 (Actions): 상태 변화 시 수행되는 동작

특징

• 명확성: 시스템의 동작을 명확하게 정의할 수 있습니다.
• 예측 가능성: 주어진 입력에 대한 시스템의 반응을 쉽게 예측할 수 있습니다.
• 테스트 용이성: 각 상태와 전이를 개별적으로 테스트할 수 있습니다.

추가적인 이미지와 예시들은 Finite State Machine에서 확인할 수 있습니다.

예시: 자동 판매기

States: 대기, 선택, 지불, 배출
Transitions:
  대기 -> 선택 (상품 버튼 누름)
  선택 -> 지불 (금액 투입)
  지불 -> 배출 (결제 완료)
  배출 -> 대기 (상품 배출 완료)

시뮬레이션에서의 활용

1. 복잡한 시스템 모델링:
   • 연속적/이산적 개념을 조합하여 hybrid 모델링이 가능합니다.
   • 유한 상태 기계를 사용하여 시스템의 주요 동작을 정의할 수 있습니다.
2. 이벤트 기반 시뮬레이션:
   • 이산적 시간 흐름과 유한 상태 기계를 결합하여 이벤트 중심의 시뮬레이션을 구현할 수 있습니다.
3. 시스템 검증:
   • 유한 상태 기계를 통해 시스템의 모든 가능한 상태와 전이를 체계적으로 검증할 수 있습니다.
4. 실시간 시스템 설계:
   • 연속적 시간 흐름을 사용하여 물리적 프로세스를 모델링하고, 유한 상태 기계로 제어 로직을 구현할 수 있습니다.

페트리넷의 구성요소와 표기법

페트리넷(Petri net)은 병렬 시스템과 분산 시스템을 모델링하는 데 사용되는 수학적 도구입니다. 이 모델은 시스템의 동적 행동을 그래픽적으로 표현할 수 있어 복잡한 시스템을 이해하고 분석하는 데 유용합니다.

페트리넷의 주요 구성요소

페트리넷은 다음과 같은 기본 요소로 구성됩니다:

1. 플레이스 (Places):
   • 원으로 표현됩니다.
   • 시스템의 상태나 조건을 나타냅니다.
   • 토큰을 포함할 수 있습니다.
2. 트랜지션 (Transitions):
   • 직사각형이나 막대로 표현됩니다.
   • 이벤트나 동작을 나타냅니다.
3. 아크 (Arcs):
   • 화살표로 표현됩니다.
   • 플레이스와 트랜지션을 연결합니다.
4. 토큰 (Tokens):
   • 검은 점으로 표현됩니다.
   • 플레이스 내에 위치하며, 시스템의 현재 상태를 나타냅니다.

표기법

페트리넷의 수학적 표현은 다음과 같습니다: PN = (P, T, F, W, M0)

• P: 플레이스의 유한 집합
• T: 트랜지션의 유한 집합
• F: 아크의 집합 (F ⊆ (P × T) ∪ (T × P))
• W: 가중치 함수
• M0: 초기 마킹 (각 플레이스의 초기 토큰 수)

이러한 표기법을 통해 복잡한 시스템의 구조와 동작을 정확하게 표현할 수 있습니다.

페트리넷의 시뮬레이션과 패턴

페트리넷은 시스템의 동적 행동을 시뮬레이션하는 데 매우 유용합니다. 시뮬레이션을 통해 시스템의 다양한 상태와 이벤트 시퀀스를 분석할 수 있습니다.

시뮬레이션 과정

1. 초기 마킹 설정: 각 플레이스에 초기 토큰 배치
2. 발사 가능한 트랜지션 확인
3. 트랜지션 발사: 입력 플레이스에서 토큰 제거, 출력 플레이스에 토큰 추가
4. 새로운 마킹 상태 기록
5. 2-4 과정 반복

주요 패턴

페트리넷에서 자주 나타나는 패턴들:

1. 순차 실행 (Sequential Execution):
   • 한 작업이 끝나면 다음 작업이 시작되는 패턴
2. 동시성 (Concurrency):
   • 여러 작업이 독립적으로 동시에 실행되는 패턴
3. 충돌 (Conflict):
   • 두 개 이상의 트랜지션이 동일한 리소스(토큰)를 필요로 하는 패턴
4. 동기화 (Synchronization):
   • 여러 동시 실행 프로세스가 특정 지점에서 만나는 패턴

이러한 패턴들을 조합하여 복잡한 시스템의 동작을 모델링할 수 있습니다.

페트리넷의 속성과 예제

페트리넷은 시스템의 다양한 특성과 속성을 분석하는 데 사용됩니다. 이를 통해 시스템의 동작을 이해하고 잠재적인 문제를 식별할 수 있습니다.

주요 속성

1. 도달 가능성 (Reachability):
   • 특정 마킹에 도달할 수 있는지 여부를 나타냅니다.
   • 시스템이 원하는 상태에 도달할 수 있는지 확인하는 데 사용됩니다.
2. 한정성 (Boundedness):
   • 각 플레이스의 토큰 수가 일정 범위 내에 있는지를 나타냅니다.
   • 시스템 리소스의 제한을 모델링하는 데 중요합니다.
3. 활성 (Liveness):
   • 시스템이 교착 상태에 빠지지 않고 계속 동작할 수 있는지를 나타냅니다.
   • 시스템의 진행 가능성을 보장합니다.
4. 가역성 (Reversibility):
   • 초기 상태로 돌아갈 수 있는지를 나타냅니다.
   • 시스템의 복구 가능성을 분석하는 데 사용됩니다.

예제: 생산자-소비자 문제

Places: P1(생산된 아이템), P2(버퍼 공간), P3(소비된 아이템)
Transitions: T1(생산), T2(소비)
초기 마킹: M0 = (0, N, 0) (N은 버퍼 크기)

아크:
P2 -> T1 (생산 조건: 버퍼 공간 있음)
T1 -> P1 (아이템 생산)
P1 -> T2 (소비 조건: 아이템 존재)
T2 -> P3 (아이템 소비)
T2 -> P2 (버퍼 공간 반환)

이 예제는 유한한 버퍼를 가진 생산자-소비자 시스템을 모델링합니다. 페트리넷을 통해 버퍼 오버플로우나 언더플로우와 같은 문제를 쉽게 식별하고 분석할 수 있습니다.

8-퀸 문제

8-퀸 문제는 체스판에 8개의 퀸을 서로 공격할 수 없게 배치하는 문제입니다. 이 문제는 조합 최적화와 백트래킹 알고리즘을 이해하는 데 자주 사용되는 예제입니다.

문제 정의

• 8x8 체스판 사용
• 8개의 퀸을 배치
• 어떤 퀸도 다른 퀸을 공격할 수 없어야 함 (같은 행, 열, 대각선에 있지 않아야 함)

해결 접근 방식

1. 백트래킹 (Backtracking):
   • 가능한 모든 배치를 시도하며, 충돌이 발생하면 이전 상태로 돌아가 다른 옵션을 시도합니다.
2. 제약 만족 문제 (Constraint Satisfaction Problem):
   • 각 퀸의 위치에 대한 제약 조건을 정의하고, 이를 만족하는 해를 찾습니다.
3. 유전 알고리즘 (Genetic Algorithm):
   • 가능한 해들의 집단을 진화시켜 최적의 해를 찾습니다.

코드 예시 (Python)

def is_safe(board, row, col):
    # 같은 열에 퀸이 있는지 확인
    for i in range(row):
        if board[i] == col:
            return False
    
    # 왼쪽 위 대각선 확인
    for i, j in zip(range(row-1, -1, -1), range(col-1, -1, -1)):
        if board[i] == j:
            return False
    
    # 오른쪽 위 대각선 확인
    for i, j in zip(range(row-1, -1, -1), range(col+1, 8)):
        if board[i] == j:
            return False
    
    return True

def solve_queens(board, row):
    if row == 8:
        print(board)
        return True
    
    for col in range(8):
        if is_safe(board, row, col):
            board[row] = col
            if solve_queens(board, row + 1):
                return True
            board[row] = -1
    
    return False

board = [-1] * 8
solve_queens(board, 0)

이 코드는 백트래킹 방식으로 8-퀸 문제를 해결합니다. 각 행에 하나의 퀸을 배치하며, 충돌이 발생하면 다른 위치를 시도합니다.

오토마타

오토마타(Automata)는 추상적인 기계 또는 계산 모델을 나타냅니다. 이는 컴퓨터 과학에서 계산 과정을 형식화하고 분석하는 데 사용되는 중요한 개념입니다.

오토마타의 종류

1. 유한 오토마타 (Finite Automata):
   • 유한한 수의 상태를 가집니다.
   • 결정적(DFA)과 비결정적(NFA) 유한 오토마타로 구분됩니다.
2. 푸시다운 오토마타 (Pushdown Automata):
   • 유한 오토마타에 스택이 추가된 형태입니다.
   • 문맥 자유 언어를 인식할 수 있습니다.
3. 튜링 머신 (Turing Machine):
   • 가장 강력한 형태의 오토마타입니다.
   • 모든 계산 가능한 함수를 계산할 수 있습니다.

유한 오토마타의 구성요소

• 상태 집합 (Q)
• 입력 알파벳 (Σ)
• 전이 함수 (δ)
• 초기 상태 (q0)
• 종결 상태 집합 (F)

응용 분야

1. 컴파일러 설계:
   • 어휘 분석기와 구문 분석기 구현에 사용됩니다.
2. 텍스트 처리:
   • 패턴 매칭과 정규 표현식 구현에 활용됩니다.
3. 프로토콜 검증:
   • 통신 프로토콜의 정확성을 검증하는 데 사용됩니다.
4. 자연어 처리:
   • 문법 구조 분석과 언어 모델링에 적용됩니다.

오토마타 이론은 계산 이론의 기초를 제공하며, 알고리즘 설계와 복잡도 분석에 중요한 역할을 합니다.